No modelo de regressão linear simples na forma matricial Y = Xβ + ε, Y denota o vetor de respostas, X representa a matriz de delineamento (ou matriz de desenho), β é o vetor de coeficientes do modelo e ε é o vetor de erros aleatórios independentes e identicamente distribuídos. Tem-se também que X´Y = e (X´X) ^-1 =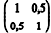 em que X´ é a matriz transposta de X. Com base nessas informações, julgue o próximo item, considerando que a variância do erro aleatório é

Se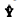 representa o modelo ajustado, então Var( 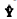) = Var(g) = σ² × I, em que I é uma matriz identidade e σ² representa a variância dos erros aleatórios.

No modelo de regressão linear simples na forma matricial Y = Xβ + ε, Y denota o vetor de respostas, X representa a matriz de delineamento (ou matriz de desenho), β é o vetor de coeficientes do modelo e ε é o vetor de erros aleatórios independentes e identicamente distribuídos. Tem-se também que X´Y = e (X´X) ^-1 =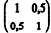 em que X´ é a matriz transposta de X. Com base nessas informações, julgue o próximo item, considerando que a variância do erro aleatório é

Se a variância de cada erro aleatório fosse igual a 4, as variâncias dos estimadores dos coeficientes do modelo seriam iguais a 2.

No modelo de regressão linear simples na forma matricial Y = Xβ + ε, Y denota o vetor de respostas, X representa a matriz de delineamento (ou matriz de desenho), β é o vetor de coeficientes do modelo e ε é o vetor de erros aleatórios independentes e identicamente distribuídos. Tem-se também que X´Y = e (X´X) ^-1 =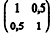 em que X´ é a matriz transposta de X. Com base nessas informações, julgue o próximo item, considerando que a variância do erro aleatório é

A estimativa do vetor de coeficientes é

No modelo de regressão linear simples na forma matricial Y = Xβ + ε, Y denota o vetor de respostas, X representa a matriz de delineamento (ou matriz de desenho), β é o vetor de coeficientes do modelo e ε é o vetor de erros aleatórios independentes e identicamente distribuídos. Tem-se também que X´Y = e (X´X) ^-1 = em que X´ é a matriz transposta de X. Com base nessas informações, julgue o próximo item, considerando que a variância do erro aleatório é

O referido modelo possui uma única variável regressora.

Um modelo de regressão linear múltipla tem a forma y = β₀ + β₁X₁ + β₂X₂ + ε, em que β₀, β₁ e β₂ são os coeficientes do modelo e ε denota o erro aleatório normal com média nula e desvio padrão σ. As variáveis regressoras X₁ e X₂ são ortogonais. O quadro a seguir mostra as estimativas dos coeficientes do modelo obtidas pelo método da máxima verossimilhança a partir de uma amostra de tamanho n = 20. Nesse quadro, para cada coeficiente β_k, k = 0,1,2, a razão t refere-se ao seu teste de significância H₀ : β_k = 0 versus H₁ : β_k ≠ 0.

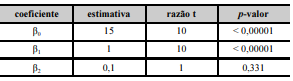
Com base nessas informações e no quadro apresentado, julgue o próximo item.

A hipótese nula H₀ : β₂ = 0 é rejeitada para o nível de significância do teste α = 5%.