Questões de Concurso
Filtrar
9.754 Questões de concurso encontradas
Página 1894 de 1.951
Questões por página:
Questões por página:
Seja F = (xz, yz, –x2) um campo vetorial em 
. Analise as declarações a seguir sobre o divergente e o rotacional de F:
I) rot F = (–y, 3x, 0)
II) div F = 2z
III) rot(div F) = 0
Está correto o que se declara em
A derivada da função f(x,y) = 2xy3 – 3x2 y no ponto (–1,2) na direção do vetor v = (1,–1) é
O polinômio de Taylor de 2º grau, centrado em a = 
, que aproxima a função f(x) = sen(x) é
Considere a transformação linear T: 
tal que T(1, 0) = (–1, 1) e T(0, 1) = (3, 2). Sendo 
os auto-valores de T, 
e reais e 
, tem-se que
Sejam u e v vetores de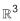 
cujos módulos são, respectivamente, 3 e 1 e que formam entre si um ângulo θ tal que cos θ = -2⁄3 . O módulo do vetor 2u – 3v é
