Questões de Concurso

Para estimar, por máxima verossimilhança (MV) ou pelo método dos momentos (MM), o único parâmetro de dada distribuição de probabilidades, seleciona-se uma amostra de tamanho n.

A função densidade da distribuição é:

f_x(x) = θx^θ-1 , para 0 < x < 1 e zero caso contrário.Além disso, considere:

Então, os estimadores de MV e de MM (com base na média da distribuição) para θ são, respectivamente:

A distribuição das alturas dos indivíduos de uma população é aproximadamente Normal, com média 1,70 m e variância 0,01. Adicionalmente, não havendo, na população, pessoas com alturas inferiores a 1,50 m nem superiores a 1,90 m, essa distribuição é truncada nos extremos.

São fornecidas também as seguintes informações:

ɸ (1)≅ 0,84 e ɸ (2) ≅ 0,98

ɸ (z) = função distribuição acumulada da Normal Padrão

Então a probabilidade de que um indivíduo da população, sorteado ao acaso, tenha altura entre 1,60 m e 1,80 m é:

Suponha que uma amostra de tamanho n = 5 é extraída de umapopulação Normal, com média desconhecida, obtendo asseguintes observações:

X1 = 2, X2 = 5, X3 = 6, X4 = 9 e X5 = 12

São dados ainda os seguintes valores, retirados da tabela da distribuição Qui-Quadrado:

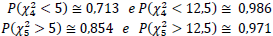
Se a população tem variância verdadeira σ2 = 4 em nova amostra (n=5), a probabilidade de se observar uma variância amostral maior do que a anterior é de:

Um fabricante de equipamentos de informática, que conhece a distribuição do tempo de vida útil dos HDs externos, precisa avaliar os gastos com serviços de garantia. Essa distribuição é a exponencial com média β = 15 anos, sendo que os HDs já vendidos têm, por hipótese, 3 anos de uso, sem apresentar defeitos. Supondo que a garantia é de 12 anos, a probabilidade de que ele tenha que prestar assistência a um determinado HD entre os vendidos é:

Suponha que uma amostra aleatória de tamanho n = 3 será extraída de uma população cuja variável a ser observada é X, tendo função de densidade teórica fx(x) =2x para 0 < x < 1 e zero caso contrário. A extração é feita com a ajuda de uma tabela de números aleatórios, com valores convertidos aos valores amostrais de X através da transformação integral de Y = Fx(x), que é a função distribuição acumulada de X. Se os valores lidos na tabela de aleatórios forem 0,25, 0,49 e 0,81, a média amostral será igual a: