Questões de Concurso
Filtrar
1.570 Questões de concurso encontradas
Página 286 de 314
Questões por página:
Considere o modelo yi = α + βxi + εi , i = 1,2,3, ... onde:
I. yi e xi representam, respectivamente, o tempo de reação a certo estímulo, em segundos, e a idade, em anos, do indivíduo i.
II. α e β representam os parâmetros desconhecidos do modelo.
III. εi representa o erro aleatório com as respectivas hipóteses para a regressão linear simples.
IV. As estimativas de α e β foram obtidas pelo método de mínimos quadrados por meio de 10 observações, utilizando-se as seguintes informações: 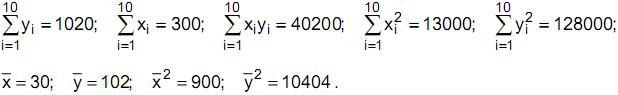
Nessas condições, a soma de quadrados residuais do modelo é igual a:
Dados: e-2 = 0,14; e-4 = 0,018
I. X é uma variável aleatória com distribuição binomial com média 2p e variância (2p-2p2).
II. Y é uma variável aleatória com distribuição binomial com média 5p e variância (5p-5p2).
III. A probabilidade de X ser inferior a 2 é igual a 15/16.
Nessas condições, a probabilidade de Y ser superior a 3 é igual a :
O Departamento de Pessoal de certo órgão público fez um levantamento dos salários, em número de salários mínimos (SM), dos seus 400 funcionários, obtendo os seguintes resultados: 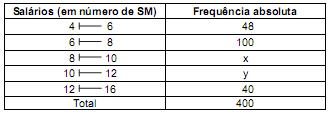
Sabe-se que a mediana dos salários desses funcionários calculada por meio dessa tabela pelo método da interpolação linear é igual a 8,8 SM. Nessas condições, o salário médio desses 400 funcionários, em número de salários mínimos, considerando que todos os valores incluídos em um intervalo de classe são coincidentes com o ponto médio do intervalo, é igual a: