2. Questões de Concurso

Filtrar

Questões por página:
Sejam Y e W variáveis aleatórias independentes, ambas com distribuição normal, com médias μy = 2 e μW = 4 e com variâncias dadas por σ2y = 9 e σ2W = 16

Sejam X1,X2,X3,...X25 variáveis aleatórias independentes e identicamente distribuídas, com E ( Xi) = 4 e (Vi ) = 9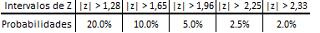



Sobre a variável Y= X1,X2,X3,...X25 e usando a tabela da normal-padrão acima é correto afirmar que:

Uma pesquisa feita junto à população carcerária levantou o perfil dos presos, observando o grau de instrução e o tempo de condenação, em valores percentuais. A função densidade de X = Grau de Instrução e Y = Tempo de Condenação é:

Assim sendo, é correto concluir que:

Seja (X,Y) uma variável bidimensional, onde X = 0 se o indivíduo é inocente e X = 1 se é culpado, enquanto Y = 0 se o indivíduo é absolvido e Y = 1 se for condenado. A função de probabilidade conjunta é dada por:

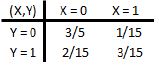
Então é correto que:

Considere uma variável aleatória do tipo contínua, cuja função de densidade de probabilidade é dada por:

fX (x) =( 1+ θ).xθ , se x ∈ (0,1) e zero caso contrário.

Sobre o momento ordinário de ordem k da distribuição de probabilidades, é possível afirmar que E ( Xk) é igual a:
© 2016-2024 Fonte Concursos - Questões de Concurso e Plano de Estudo