Seja o modelo linear de análise de covariância Y_i = α + βD_i + γX_i + ε_i referente a um determinado ramo de atividade. Y_i representa o salário anual de um empregado i, X_i é o número de anos de experiência do empregado i e ei é o erro aleatório com as respectivas hipóteses da correspondente regressão (a, ß e γ são parâmetros desconhecidos). Com relação a este modelo, dado que D_i = 1 se o empregado i for homem e D_i = 0 se o empregado i for mulher, pode-se afirmar que

Todos os funcionários de 5 grupos de trabalho com 6 funcionários cada um, escolhidos aleatoriamente, são designados para realizar uma tarefa, independentemente. O tempo que cada um dos 30 funcionários levou para concluir a tarefa é anotado. Deseja-se saber, a um determinado nível de significância, se os tempos médios dos grupos para a realização da tarefa são iguais. Considere algumas informações do quadro de análise de variância: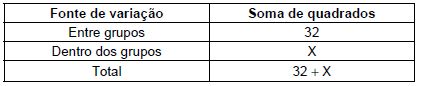



Se o valor da estatística F (F calculado) utilizado para testar a igualdade dos tempos médios apresentou um valor igual a 20, então X é igual a

Seja o modelo de regressão linear múltipla  de uma certa população, em que:

I. Y_i é variável dependente,

II. X₁ e X₂ são as variáveis explicativas,

III. a, ß e γ são parâmetros desconhecidos,

IV. ε_i o erro aleatório com as respectivas hipóteses do modelo de regressão linear múltipla,

V. i é a i-ésima observação,

VI. n é o número de observações.

Considere que n = 20 e que as estimativas de a, ß e γ foram obtidas pelo método dos mínimos quadrados. O valor da estatística F (F calculado) utilizado para testar a existência da regressão, a um determinado nível de significância apresentou um valor igual a 31,5. O poder de explicação deste modelo (R²), definido como sendo o resultado da divisão da respectiva variação explicada pela variação total, é igual a

Se são as médias das observações de X e Y, respectivamente), então a variação explicada pelo modelo é igual a