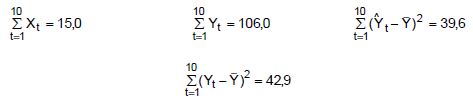60 Questões de concurso encontradas
Página 5 de 12
Questões por página:
Considerando o quadro da análise de variância, obtém-se que o coeficiente de determinação (R2), definido como sendo o quociente da divisão da variação explicada devido à regressão pela variação total, é tal que
Em uma região, suspeita-se que a escolha entre duas profissões P1 e P2 dependa do sexo das pessoas. Nenhuma pessoa pode exercer simultaneamente P1 e P2. Dentre as pessoas que exercem estas duas profissões, foram formados dois grupos, o primeiro com 80 homens e o segundo com 120 mulheres, obtendo-se o seguinte resultado: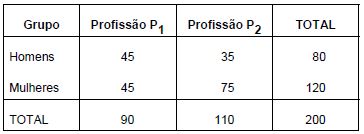
Utilizando o teste qui-quadrado a um nível de significância α tem-se que o valor crítico da distribuição qui-quadrado com 1 grau de liberdade é superior ao valor do qui-quadrado observado. Então, o valor do qui-quadrado observado e a conclusão com relação à escolha da profissão a um nível de significância α são
Com o objetivo de comprovar se dois grupos independentes diferem em tendências centrais, um analista utiliza a tabela abaixo formulando as hipóteses:
H0: Os 2 grupos provêm de populações com a mesma mediana (hipótese nula).
H1: A mediana de um grupo difere da mediana do outro grupo (hipótese alternativa).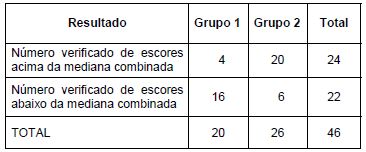
Então, é correto afirmar que
Os lucros brutos anuais das empresas de um determinado ramo de atividade apresentam uma distribuição normal com média μ e variância populacional σ2 desconhecidas. A partir de uma amostra aleatória de tamanho 25 da população considerada de tamanho infinito, deseja-se testar a hipótese H0: μ = 20 milhões de reais contra a alternativa H1: μ > 20 milhões de reais, com a realização do teste t de Student. A média e o desvio padrão da amostra são iguais a 23 e 8, respectivamente, em milhões de reais. Seja tc o valor calculado correspondente para comparar com o valor tabelado tt da distribuição t de Student, com n graus de liberdade, ao nível de significância α. Então, é correto afirmar que
Um fabricante faz dois tipos de lâmpadas. Seja X a variável aleatória que representa o tempo de vida do primeiro tipo e Y a variável aleatória que representa o tempo de vida do segundo tipo. Sabe-se que X e Y são independentes e que os respectivos desvios padrões populacionais dos dois tipos são iguais a 250 horas, cada um. Um comprador testou 36 lâmpadas do tipo X e 64 lâmpadas do tipo Y, obtendo 1.000 horas e 1.200 horas de duração média para o tipo X e o tipo Y, respectivamente. Foram formuladas as seguintes hipóteses: H0: μx = μy (hipóteses nula, isto é, a vida média dos tipos X e Y é a mesma) e H1: μx ≠ μy (hipótese alternativa). Considerou-se para o teste que o tamanho das populações é infinito, além de serem normalmente distribuídas e que na distribuição normal padrão (Z) a probabilidade P (Z ≥ zα) = α (0 < α 0,5). Então, pode-se afirmar que a um nível de significância de 2 α