Questões de Concurso

Considere a transformação linear f:R2→R3, tal quef(1, 2)=(2, 1, 1) e f(1, −1)=(−1, −2, 1) . Qual é o vetor v ∈ R2 tal que f(v)=(7, 4, 3) ?

Seja V o espaço vetorial dos polinômios f de grau menor ou igual a 4, isto é, f(x)= 4∑n=0​ fn​xn, onde fn​ ∈ R.

Qual é a dimensão do espaço nulo da transformação linear dada por

T:V →R3

f ↦ (f(−1), f(0), f(1)) ?

Considere o operador linear f:R2→R2, cuja representação matricial na base canônica A={(1, 0), (0, 1)} do R2 é dada por TA​= [3−2​−34​], e seja a base B={(3, 2), (1, 1)} outra base do R2 .

Qual é a representação matricial TB​ do operador f na base B ?

Considere os vetores u=(1, 3, −4) e v=(−2, 2, 7) do R3 .

Qual é o valor de m para que o vetor η =(11, 9, m) seja a combinação linear de u e v ?

O losango abaixo, de vértices (0,0), (-3, -1), (0, -2), (3, -1), gira uma volta completa no eixo x, gerando um sólido de revolução.

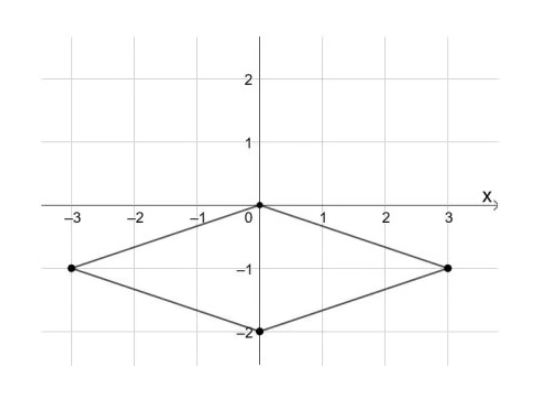
Conforme a figura acima, quais são os valores da área da superfície (A) e do volume do sólido formado (V), respectivamente?