Seja Z_t um processo AR(1) estacionário dado por Z_t = Φ Z_t−1 + a_t , onde at é o ruído branco de média zero e variância σ² . Considere as seguintes afirmações relativas a Z_t :

I. Sua região de admissibilidade é |Φ| > 1.
II. Sua função de autocorrelação decai exponencialmente.
III. A previsão de origem t e horizonte h (h > 0) é Φ^hZ_t , onde Z é o valor da série no instante t.
IV. Sua função de densidade espectral é  σ² / 2π

Considere as afirmações abaixo, relativas às técnicas de Análise Multivariada:

I. Na análise de correlação canônica, a ideia básica é resumir a informação de cada conjunto de variáveis resposta em combinações lineares, sendo que a escolha dos coeficientes dessas combinações deve ter como critério a minimização da correlação entre os conjuntos de variáveis resposta.

II. A análise de correspondência é adequada quando se quer examinar a relação entre variáveis categóricas nominais ou entre categorias dessas variáveis.

III. A análise de regressão múltipla é exemplo de uma técnica de interdependência.

É correto o que consta APENAS em

Suponha que temos 7 provas independentes com probabilidade de sucesso 0,4. Seja X a variável aleatória que representa o número total de sucessos nessas 7 provas e Y a variável aleatória que representa o número de sucessos nas 4 primeiras provas. Então, a probabilidade condicional expressa por
P (Y = 2 | X = 5) é igual a:

Na venda de uma partida de 10.000 peças, o vendedor recebe a seguinte proposta do comprador A: Este examinará uma amostra aleatória de n = 100 peças e pagará R$ 10,00 por peça, se houver até duas defeituosas na amostra e pagará R$ 5,00 por peça, caso contrário. Se 4% de todas as peças são defeituosas, o valor médio que o comprador A se propõe a pagar por peça, calculado quando se faz uso da aproximação de Poisson para as probabilidades necessárias ao cálculo do referido valor médio, é, em reais, igual a

Dados:
e^-4 = 0,018
e^-5 = 0,007

Seja 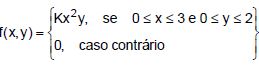, a função densidade de probabilidade da variável aleatória bidimensional
contínua (X,Y). Nessas condições, P(0 ≤ X ≤ 2, 1 < Y ≤ 2) é igual a: