Questões da prova:
FCC - 2015 - TRT - 3ª Região (MG) - Analista Judiciário - Estatística
limpar filtros
60 Questões de concurso encontradas
Página 5 de 12
Questões por página:
Questões por página:
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
Para um determinado ramo de atividade, o modelo linear correspondente à equação Yi = α + βXi + γSi + ϵi (i = 1, 2, 3, ...) foi construído para estimar o salário mensal (Yi), em reais, em função do número de anos de experiência (Xi) e do sexo (Si) do trabalhador (i refere-se ao i-ésimo trabalhador). Considera-se no modelo que Si = 1 se o trabalhador for homem e Si = 0 se o trabalhador for mulher. Os parâmetros α, β e γ são desconhecidos e ϵi é o erro aleatório com as respectivas hipóteses da correspondente regressão. As estimativas de α, β e γ (a, b e c, respectivamente) foram obtidas pelo método dos mínimos quadrados com base em n observações e todas foram estritamente positivas. Considerando todos os trabalhadores deste ramo de atividade e utilizando a função obtida 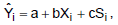
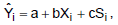
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
Um modelo regressivo linear múltiplo correspondente à equação Zi = α + βXi + γYi + ϵi (i = 1, 2, 3, ... ) foi construído para prever Z em função de X e Y. Os parâmetros α, β e γ são desconhecidos, ϵi corresponde ao erro aleatório com as respectivas hipóteses do modelo de regressão linear múltipla e i refere-se à i-ésima observação. Com base em 21 observações e utilizando o método dos mínimos quadrados obtiveram-se as estimativas de α, β e γ (a, b e c, respectivamente).

O valor da estatística F (F calculado) que permite decidir por meio da comparação com o F tabelado sobre a existência da regressão é igual a
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
mostrar texto associado
Pelo quadro de análise de variância correspondente e considerando que 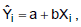
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
mostrar texto associado
Considerando a equação da reta obtida pelo método dos mínimos quadrados, obtém-se que o acréscimo do faturamento bruto, em milhões de reais, cada vez que se decide aumentar em 1 milhão de reais o dispêndio com material promocional é de
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
Em uma pesquisa realizada na empresa Alfa com 40 funcionários escolhidos aleatoriamente, com reposição, observou-se que 26 apresentavam uma idade superior a 30 anos. Atribuiu-se 26 sinais positivos para os que apresentaram uma idade superior a 30 anos e 14 sinais negativos para o restante (observação: nenhum funcionário apresentou a idade de 30 anos). Decide-se aplicar o teste do sinal para averiguar se a proporção populacional de sinais positivos (p) é igual a 50%, a um nível de significância de 5%. Foram formuladas as hipóteses H0: p = 50% (hipótese nula) e H1: p≠50% (hipótese alternativa). Com a aproximação da distribuição binomial pela normal, sem a correção de continuidade, foi apurado o valor do escore reduzido k correspondente para comparação com o valor crítico z da distribuição normal padrão (Z) tal que P(│Z│ ≤ z) = 95%. O valor de k é tal que