Questões da prova:
FCC - 2015 - TRT - 3ª Região (MG) - Analista Judiciário - Estatística
limpar filtros
60 Questões de concurso encontradas
Página 6 de 12
Questões por página:
Questões por página:
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
Em duas grandes empresas E1 e E2 são selecionados aleatoriamente 50 empregados de E1 e 150 empregados de E2. Foi perguntado a cada um dos empregados se eles eram a favor da substituição dos equipamentos da sua empresa. Supondo que esta pesquisa tenha sido realizada independentemente, o resultado pode ser visualizado pela tabela abaixo.
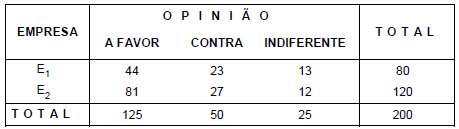
Com base nos dados desta tabela, deseja-se testar, ao nível de significância de 10%, se a opinião dos empregados depende da empresa em que trabalham. Utilizou-se então o teste qui-quadrado para esta tomada de decisão.

Conclui-se que, ao nível de significância de 10%, a opinião dos empregados
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
De uma população normal e de tamanho infinito com o desvio padrão populacional igual a 4 extrai-se uma amostra aleatória de tamanho 64. Com base nesta amostra, deseja-se saber, ao nível de significância de 5%, se a média μ desta população é inferior a 30. Foram formuladas as hipóteses H0: μ = 30 (hipótese nula) e H1: μ < 30 (hipótese alternativa) com utilização das informações da curva normal padrão (Z) que as probabilidades P(Z > 1,64) = 0,05 e P(Z > 1,28) = 0,10. O menor valor encontrado para a média amostral 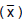 tal que H0 não é rejeitada apresenta um valor igual a
tal que H0 não é rejeitada apresenta um valor igual a
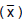 tal que H0 não é rejeitada apresenta um valor igual a
tal que H0 não é rejeitada apresenta um valor igual a
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
A probabilidade de ocorrência de um evento em uma determinada experiência é igual a p. Considerando as hipóteses 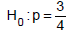 (hipótese nula) e
(hipótese nula) e 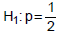 (hipótese alternativa) determina-se que H0 será aceita se e somente se o evento ocorrer em pelo menos 4 vezes em uma série de 5 experiências executadas. A potência deste teste é igual a
(hipótese alternativa) determina-se que H0 será aceita se e somente se o evento ocorrer em pelo menos 4 vezes em uma série de 5 experiências executadas. A potência deste teste é igual a
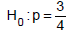 (hipótese nula) e
(hipótese nula) e 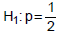 (hipótese alternativa) determina-se que H0 será aceita se e somente se o evento ocorrer em pelo menos 4 vezes em uma série de 5 experiências executadas. A potência deste teste é igual a
(hipótese alternativa) determina-se que H0 será aceita se e somente se o evento ocorrer em pelo menos 4 vezes em uma série de 5 experiências executadas. A potência deste teste é igual a
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
A amostra aleatória { X1, X2, X3, ... , X9 } foi extraída de uma população normal de tamanho infinito com variância (σ2) desconhecida.
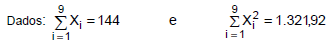
Com base nesta amostra, deseja-se obter um intervalo de confiança de 90% para a média μ da população utilizando a distribuição t de Student levando em conta a tabela a seguir.

Este intervalo é igual a
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
Uma amostra aleatória de tamanho 225 é extraída de uma população (P1) normalmente distribuída e de tamanho infinito. Sabe-se que a variância de P1 é igual a 64. Com base nesta amostra, um intervalo de confiança de nível (1 − α) foi construído para a média μ' de P1 e foi igual a [28,64 ; 31,36]. Em uma outra população (P2), independente da primeira, também normalmente distribuída e de tamanho infinito com média μ'', obteve-se com base em uma amostra aleatória de tamanho 400 um intervalo de confiança de nível (1 − α) para μ'' igual a [20,286 ; 21,714]. O desvio populacional de P2 é igual a