Questões da prova:
FCC - 2015 - TRT - 3ª Região (MG) - Analista Judiciário - Estatística
limpar filtros
60 Questões de concurso encontradas
Página 2 de 12
Questões por página:
Questões por página:
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
O modelo abaixo foi ajustado a uma série temporal de produção de certo produto:
Zt = at + 0,5Zt−1 + 0,5at−1 , t = 1,2, ...
onde at é o ruído branco de média zero e variância 3.
Considere:
I. As condições de estacionariedade e invertibilidade de Zt estão satisfeitas.
II. As funções de autocorrelação e autocorrelação parcial de Zt decaem exponencialmente após o lag 1.
III. A variância de Zt é igual a 7.
IV. A função de autocorrelação de Zt independe do valor da variância do ruído.
Está correto o que consta em
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
Sabe-se que a função de distribuição conjunta das variáveis X e Y é dada por
Nessas condições, P(0,3 < X < 0,7) é, em %, igual a
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
mostrar texto associado
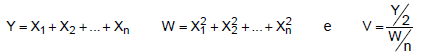
Sejam X1, X2, ... , Xn variáveis aleatórias independentes e identicamente distribuídas com distribuição normal padrão. Sejam as variáveis aleatórias:
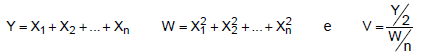
Considere:
I. A função geratriz de momentos de Y, quando n = 2, é m(t) = e2t .
II. A variável W tem distribuição qui-quadrado com (n − 1) graus de liberdade.
III. A variável V tem distribuição F de Snedecor com graus de liberdade 2 e n.
IV. Para n = 4, P(− 2 < Y < 1) = 0,432.
Está correto o que consta APENAS em
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
mostrar texto associado
O tempo total para a análise de um processo trabalhista, que chega a um Tribunal Regional do Trabalho, é dado pela soma dos tempos dos 3 analistas, que o examinam. Sejam Xi, i = 1,2,3, as variáveis aleatórias que representam os tempos, em dias, para análise dos analistas 1,2 e 3, respectivamente. Sabe-se que o vetor 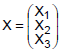 tem distribuição normal multivariada com vetor de médias dado por
tem distribuição normal multivariada com vetor de médias dado por 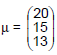 e matriz de covariâncias dada por
e matriz de covariâncias dada por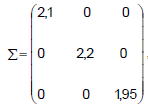 , onde os valores do vetor μ, são dados em dias e os da matriz Σ em (dias)2.
, onde os valores do vetor μ, são dados em dias e os da matriz Σ em (dias)2.
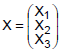 tem distribuição normal multivariada com vetor de médias dado por
tem distribuição normal multivariada com vetor de médias dado por 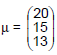 e matriz de covariâncias dada por
e matriz de covariâncias dada por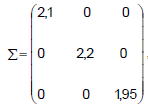 , onde os valores do vetor μ, são dados em dias e os da matriz Σ em (dias)2.
, onde os valores do vetor μ, são dados em dias e os da matriz Σ em (dias)2. Um processo é selecionado aleatoriamente dentre todos os processos que chegam àquele órgão. A probabilidade do tempo total para análise se situar entre 42 dias e 45 dias, em %, é igual a
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
mostrar texto associado
Considere que X é a variável aleatória, que representa as idades, em anos, dos trabalhadores de certa indústria. Suponha que X têm distribuição normal com média de μ anos e desvio padrão de 5 anos.
Uma amostra aleatória, com reposição, de 16 trabalhadores será selecionada e sejam X1, X2, ...X16 as idades observadas e 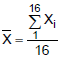 a média desta amostra. Sabendo-se que a probabilidade de X ser superior a 30 anos é igual a 0,919, o valor de μ, em anos, é igual a
a média desta amostra. Sabendo-se que a probabilidade de X ser superior a 30 anos é igual a 0,919, o valor de μ, em anos, é igual a
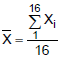 a média desta amostra. Sabendo-se que a probabilidade de X ser superior a 30 anos é igual a 0,919, o valor de μ, em anos, é igual a
a média desta amostra. Sabendo-se que a probabilidade de X ser superior a 30 anos é igual a 0,919, o valor de μ, em anos, é igual a