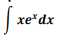Questões da prova:
Instituto Exata - 2024 - Prefeitura de Alvorada do Oeste - RO - Professor - Matemática
limpar filtros
40 Questões de concurso encontradas
Página 1 de 8
Questões por página:
Questões por página:
Concurso:
Prefeitura de Alvorada do Oeste - RO
Disciplina:
Matemática
Em um sistema de controle de movimentos periódicos, a posição de um objeto oscilante é modelada pela equação √3 ∗ cos(x) + sen(x) = 1. Determine os valores de x ∈ ℝ que satisfazem essa equação, considerando a natureza periódica do movimento.
Concurso:
Prefeitura de Alvorada do Oeste - RO
Disciplina:
Matemática
Uma fábrica utiliza uma esteira para transportar produtos que precisam passar por um controle de qualidade. A velocidade da esteira, em metros por segundo, é modelada pela função f(x), onde x representa a posição do produto ao longo da esteira, em metros. A velocidade é definida da seguinte maneira:
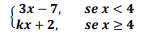
Para garantir um transporte suave dos produtos, é necessário que a velocidade da esteira não tenha variações bruscas exatamente no ponto x = 4. Calcule o valor de k que torna a função contínua.
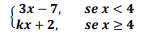
Para garantir um transporte suave dos produtos, é necessário que a velocidade da esteira não tenha variações bruscas exatamente no ponto x = 4. Calcule o valor de k que torna a função contínua.
Concurso:
Prefeitura de Alvorada do Oeste - RO
Disciplina:
Matemática
Uma empresa agrícola está estudando a produtividade de sua plantação em função do tempo de irrigação. A produtividade, P(t), em toneladas por hectare, é modelada pela seguinte função:
P(t) =〖-2t〗^3 + 〖6t〗^2 + 12t
Onde t representa o tempo de irrigação em horas. A empresa deseja determinar o tempo de irrigação que maximiza a produtividade e, se houver, identificar o tempo que corresponde à mínima produtividade dentro de um intervalo de tempo. Qual é o tempo aproximado de irrigação que maximiza a produtividade e qual é o valor máximo de produtividade?
P(t) =〖-2t〗^3 + 〖6t〗^2 + 12t
Onde t representa o tempo de irrigação em horas. A empresa deseja determinar o tempo de irrigação que maximiza a produtividade e, se houver, identificar o tempo que corresponde à mínima produtividade dentro de um intervalo de tempo. Qual é o tempo aproximado de irrigação que maximiza a produtividade e qual é o valor máximo de produtividade?
Concurso:
Prefeitura de Alvorada do Oeste - RO
Disciplina:
Matemática
Um carpinteiro está construindo uma caixa de madeira retangular e precisa calcular seu volume. Ele sabe que a área total das superfícies da caixa deve ser de 720 cm² para economizar material. Além disso, a soma das três dimensões da caixa é de 34 cm, e a diagonal de uma das faces mede 20 cm. Com essas informações, ele deseja determinar o volume exato da caixa.
Concurso:
Prefeitura de Alvorada do Oeste - RO
Disciplina:
Matemática
Calcule a integral por partes da função: