Se a variável aleatória X tem distribuição normal com média μ e variância σ²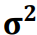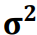, ou seja, X ⁓ N(μ, σ²), _s2 = 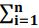(x_i–x̄)²/n–1 (variância amostral) é a estimativa de σ² com base em uma amostra com n observações, [x₁, x₂, ..., x_n]. Assim, a variável T = X – μ/s tem distribuição t de Student com n – 1 graus de liberdade, ou seja, T ~ t_n-1. Nesse caso, sabendo que P(T ≤ 2) = 0,968027 e P(T ≥ -2) = 0,031973, é correto afirmar que

Um estatístico conduziu um experimento para verificar se existem diferenças estatisticamente significativas entre os resultados quantitativos de três procedimentos aplicados em amostras independentes. Os resultados obtidos com o experimento são:

Tabela da Análise da Variância – ANOVA

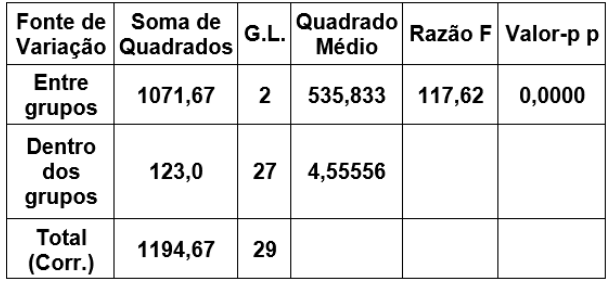
Teste de Levene para hipótese de variâncias iguais

Teste de Normalidade para os resíduos da ANOVA

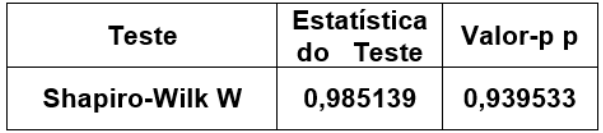
Teste de Kruskal-Wallis para hipótese de medianas iguais

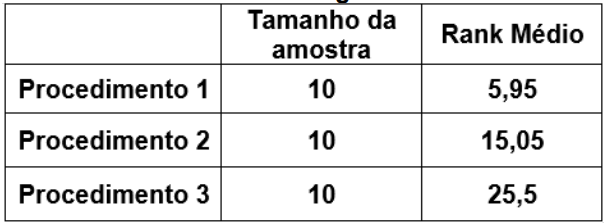
Estatística do Teste = 24,8078 Valor-p p = 0,0000041025

Então, é correto afirmar, em relação ao nível de significância de 5%, que

A Razão das Chances é definida pela razão entre a probabilidade de sucesso e a probabilidade de insucesso, ou seja, p/1–p. Então, assumindo y = β₀ + β₁X₁ + ... + β_p-1X_p-1 = X' β , tem-se no Modelo Logístico p = p(X) = p(X₁, X₂, ..., X_p-1) = e^y/e^y+1 = 1/1+e^-y= 1/1+e^-x'β. Portanto, a Razão das Chances no Modelo Logístico é

O estatístico que trata da análise de dados referentes à Justiça Federal necessita conduzir um estudo que requer informações sobre determinada característica quantitativa, X, dos processados em determinada Vara Federal. Um dos objetivos é construir um intervalo de 95% de confiança para o valor médio da característica quantitativa do grupo de processados, com erro de amostragem ou precisão de 0,5 σ, meio desvio-padrão. Ele tomou, então, uma amostra aleatória piloto de tamanho n₀ = 5 que forneceu as seguintes estatísticas amostrais, média e variância, para a característica: x̄₀ = 127,6 e S = 1290,8. A respeito das informações anteriores, sabe-se que é possível assumir o modelo de distribuição normal para a característica quantitativa do grupo de processados, que é finito com N = 2000 indivíduos e com variância desconhecida. Assim, conhecendo o escore da distribuição t de t₄ (0,975) = 2,78, é correto afirmar que o tamanho definitivo da amostra n é