Suponha que a série sem a componente sazonal tenha sido ajustada por modelos ARIMA, cujos resultados se encontram na tabela abaixo, em que 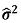representa a estimativa da variância do processo, log-veross é o valor do logaritmo da função de verossimilhança e AIC é o critério de informação de Akaike.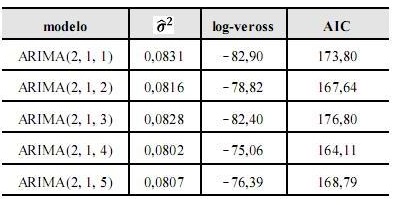



Considerando-se essas informações, é correto afirmar que o modelo sugerido para o ajuste dessa série temporal é o ARIMA(2, 1, 4).

Suponha que p = 3 e que os autovalores da matriz Ω sejam λ1 = 2,01, λ2 = 0,95 e λ3 = 0,04. Nessa situação, o número ideal de fatores que devem ser empregados para explicar a variabilidade total é igual a 2.

Se p = 5 e se os autovalores da matriz Ω forem λ₁ = 2,91, λ₂ = 1,72, λ₃ = 0,27, λ₄ = 0,10 e λ₅ < 0,01, então uma análise fatorial feita pelo método dos componentes principais indica que os dois primeiros fatores conjuntamente explicam menos de 90% da variabilidade total.

Considere que uma matriz Ω, 2 × 2, referente a um vetor aleatório (X, Y)', possua autovalores λ₁ = 1,34² e λ₂ = 0,46², e os respectivos autovetores associados a esses autovalores sejam v' = (0,7; 0,7) e u' = (-0,7; 0,7). Nesse caso, os fatores correspondentes são, respectivamente, F₁ = 1,26X + 1,26Y e F₂ = -0,15X + 0,15Y.

Em uma amostra x₁, x₂, ..., x_n, em que x_i ∈ N e n é ímpar, a mediana é um número inteiro.