Questões de Concurso
Filtrar
8.576 Questões de concurso encontradas
Página 10 de 1.716
Questões por página:
Questões por página:
Concurso:
Prefeitura de Água Boa - MT
Disciplina:
Matemática
Sejam m, n e p, constantes complexas de modo que o polinômio 2x4 + x³ + mx² + nx + p seja divisível por (x – 1)². Portanto, p é igual a:
Concurso:
Prefeitura de Água Boa - MT
Disciplina:
Matemática
A sucessão numérica (1,1,2,3,5,8,13, ...) mostra os sete primeiros termos da Sequência de Fibonacci. Nela, cada termo, a partir do terceiro, é igual a soma dos dois termos imediatamente anteriores a ele. Essa sequência possui muitas propriedades interessantes, e uma delas, descoberta por Charles Raine, está relacionada aos triângulos pitagóricos, ou seja, a um triângulo retângulo cujos três lados são números inteiros. Tomando-se quatro termos consecutivos dessa sequência, o produto dos termos extremos e o dobro do produto dos termos centrais são catetos de um triângulo pitagórico.
Logo, tomando-se o 5º,6º,7º e 8º termos da sequência de Fibonacci, pode-se obter os catetos de um triângulo retângulo cujo produto da altura relativa à hipotenusa pela própria hipotenusa é igual a:
Logo, tomando-se o 5º,6º,7º e 8º termos da sequência de Fibonacci, pode-se obter os catetos de um triângulo retângulo cujo produto da altura relativa à hipotenusa pela própria hipotenusa é igual a:
Concurso:
Prefeitura de Água Boa - MT
Disciplina:
Matemática
Considere duas urnas, A e B, de modo que a urna A contenha em seu interior duas bolas azuis e duas bolas vermelhas e que a urna B contenha três bolas azuis e três bolas vermelhas. Se P1 é a probabilidade de Rangel retirar, ao acaso e sem reposição, duas bolas de cores diferentes da urna A, e P2 a probabilidade de Rangel retirar, ao acaso e sem reposição, duas bolas de cores diferentes da urna B, a razão P2/P1 é:
Concurso:
Prefeitura de Água Boa - MT
Disciplina:
Matemática
Considere o número natural N, que representa o resultado da expressão 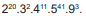 A soma dos algarismos de N + 2024 é igual a:
A soma dos algarismos de N + 2024 é igual a:
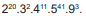 A soma dos algarismos de N + 2024 é igual a:
A soma dos algarismos de N + 2024 é igual a:
Concurso:
Prefeitura de Água Boa - MT
Disciplina:
Matemática
No plano cartesiano ortogonal, a reta y = x + m tangencia a circunferência de equação (x – 1)² + y² = 4. A soma dos possíveis valores reais de m é igual a: