Questões de Concurso
Filtrar
8.563 Questões de concurso encontradas
Página 9 de 1.713
Questões por página:
Questões por página:
Concurso:
Prefeitura de Água Boa - MT
Disciplina:
Matemática
Espera-se que, ao finalizar o Ensino Fundamental, um aluno desenvolva habilidades que o permita identificar situações de utilização da Matemática para obter soluções de problemas. Uma dessas habilidades está assim descrita no texto da BNCC:
“Reconhecer vistas ortogonais de figuras espaciais e aplicar esse conhecimento para desenhar objetos em perspectiva.”
A habilidade descrita acima está relacionada a um objeto de conhecimento do seguinte ano do Ensino Fundamental:
“Reconhecer vistas ortogonais de figuras espaciais e aplicar esse conhecimento para desenhar objetos em perspectiva.”
A habilidade descrita acima está relacionada a um objeto de conhecimento do seguinte ano do Ensino Fundamental:
Concurso:
Prefeitura de Água Boa - MT
Disciplina:
Matemática
A figura a seguir mostra um tetraedro regular VABC, cujo volume é igual a 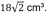
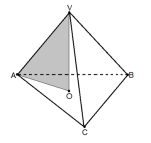
Se o ponto O representa o centro da baseABC, a área do triângulo VOA, em cm², corresponde a:
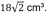

Se o ponto O representa o centro da baseABC, a área do triângulo VOA, em cm², corresponde a:
Concurso:
Prefeitura de Água Boa - MT
Disciplina:
Matemática
Considere o quadrilátero convexo ABCD, representado a seguir, e admita que os pontos E e F pertençam, respectivamente, aos segmentos AF e CB. 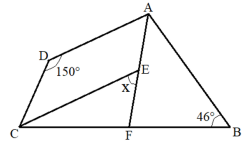
Se AF e CE representam, respectivamente, as bissetrizes dos ângulos A e C, a medida, em graus, do ângulo x é

Se AF e CE representam, respectivamente, as bissetrizes dos ângulos A e C, a medida, em graus, do ângulo x é
Concurso:
Prefeitura de Água Boa - MT
Disciplina:
Matemática
Sejam m, n e p, constantes complexas de modo que o polinômio 2x4 + x³ + mx² + nx + p seja divisível por (x – 1)². Portanto, p é igual a:
Concurso:
Prefeitura de Água Boa - MT
Disciplina:
Matemática
A sucessão numérica (1,1,2,3,5,8,13, ...) mostra os sete primeiros termos da Sequência de Fibonacci. Nela, cada termo, a partir do terceiro, é igual a soma dos dois termos imediatamente anteriores a ele. Essa sequência possui muitas propriedades interessantes, e uma delas, descoberta por Charles Raine, está relacionada aos triângulos pitagóricos, ou seja, a um triângulo retângulo cujos três lados são números inteiros. Tomando-se quatro termos consecutivos dessa sequência, o produto dos termos extremos e o dobro do produto dos termos centrais são catetos de um triângulo pitagórico.
Logo, tomando-se o 5º,6º,7º e 8º termos da sequência de Fibonacci, pode-se obter os catetos de um triângulo retângulo cujo produto da altura relativa à hipotenusa pela própria hipotenusa é igual a:
Logo, tomando-se o 5º,6º,7º e 8º termos da sequência de Fibonacci, pode-se obter os catetos de um triângulo retângulo cujo produto da altura relativa à hipotenusa pela própria hipotenusa é igual a: