Questões de Concurso
Filtrar
520 Questões de concurso encontradas
Página 64 de 104
Questões por página:
O Departamento de RH de um órgão público colheu informações sobre a variável X, que representa o tempo para a realização de determinada tarefa. Para a realização da pesquisa foi colhida uma amostra aleatória, sem reposição, de tamanho n da população de 100 funcionários que realizam a tarefa, observando-se os valores de X obtidos. Sejam Xi = tempo que o funcionário i leva para realizar a tarefa, i = 1,2,3,...,n, e 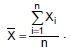 Sabendo-se que a variância de X é igual 1/11 da variância de X , o valor de n é igual a
Sabendo-se que a variância de X é igual 1/11 da variância de X , o valor de n é igual a
I. Os juízes A e B receberam, cada um, 30% dos processos que chegaram e os juízes C e D receberam, cada um, 20%.
II. Dos processos recebidos por A, B, C e D, respectivamente, 30%, 15%, 20% e 10%, receberam parecer no mesmo mês em que foram recebidos, ou seja, abril de 2014.
Um processo foi escolhido ao acaso dentre os recebidos em abril de 2014 e sabe-se que ele recebeu um parecer neste mesmo mês. A probabilidade de ele ter sido analisado pelo juiz A ou B é igual a
O seguinte modelo foi ajustado a uma série temporal de vendas de um produto:![]() onde Φ1 e Φ2 são os parâmetros do modelo e at é o ruído branco de média zero e variância 1.
onde Φ1 e Φ2 são os parâmetros do modelo e at é o ruído branco de média zero e variância 1.
Considere as afirmações:
Tal modelo é
I. estacionário se |Φ1| ≤ 1 e |Φ2| ≤ 1.
II. invertível se |Φ1| ≤ 1 e |Φ2| ≤ 1.
III. um ARMA(2,1).
IV. não estacionário, se Φ1 = 0,4 e Φ2 = 0,6 .
Está correto o que consta APENAS em
Dados:
e-2 = 0,135
e-4 = 0,018