Questões de Concurso

Um modelo de regressão linear múltipla, com intercepto, consiste em uma variável dependente, 4 variáveis explicativas e o erro aleatório com as respectivas hipóteses do modelo de regressão linear múltipla. Com base em 21 observações e utilizando o método dos mínimos quadrados obtiveram-se as estimativas dos parâmetros deste modelo. Dado que a variação total foi igual a 100 e a estimativa da variância do modelo foi igual a 1,25, então o valor da estatística F (F calculado) utilizado para testar a existência da regressão, a um determinado nível de significância, foi igual a

Atenção: Para responder à questão considere um estudo com o objetivo de obter a relação entre duas variáveis X e Y por meio do modelo Yi = α + βXi + ∈i , em que i corresponde à i-ésima observação de X e Y. Os parâmetros α e β são desconhecidos e ∈i é o erro aleatório com as respectivas hipóteses consideradas para a regressão linear simples. Com base em 20 pares de observações (Xi , Yi ), i = 1, 2, ..., 20 e utilizando o método dos mínimos quadrados foram obtidas as estimativas para α e β.

Atenção: Para responder à questão considere um estudo com o objetivo de obter a relação entre duas variáveis X e Y por meio do modelo Yi = α + βXi + ∈i , em que i corresponde à i-ésima observação de X e Y. Os parâmetros α e β são desconhecidos e ∈i é o erro aleatório com as respectivas hipóteses consideradas para a regressão linear simples. Com base em 20 pares de observações (Xi , Yi ), i = 1, 2, ..., 20 e utilizando o método dos mínimos quadrados foram obtidas as estimativas para α e β.

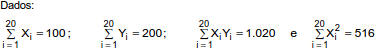
Considerando a equação da reta obtida pelo método dos mínimos quadrados, tem-se que o valor para X tal que Y = 15 é

Em três grandes cidades de um estado foram escolhidos aleatoriamente, em cada uma, 100 eleitores. Deseja-se saber, ao nível de significância α, se o grau de satisfação do desempenho do governador depende da cidade onde os eleitores residem. Em cada cidade foi perguntado, independentemente, para cada eleitor o que ele achava do desempenho do governador. A tabela abaixo reproduz o resultado da pesquisa e sabe-se que nenhum eleitor reside em mais de uma cidade.

Utilizou-se o teste qui-quadrado para concluir se existe dependência do grau de desempenho com relação às cidades e verificou-se que o qui-quadrado observado foi inferior ao qui-quadrado tabelado, de acordo com o nível de significância α estabelecido. Com relação ao teste,

Considere uma população e uma amostra aleatória respectiva de tamanho n representando toda esta população. A metodologia bootstrap é um tipo de reamostragem consistindo em gerar novas amostras