Questões da prova:
FCC - 2015 - TRT - 3ª Região (MG) - Analista Judiciário - Estatística
limpar filtros
60 Questões de concurso encontradas
Página 1 de 12
Questões por página:
Questões por página:
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
Considere:
I. Se a função geratriz de momentos da variável aleatória X for 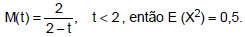
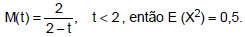
II. Se X e Y são variáveis aleatórias com distribuição normal, a distribuição conjunta de X e Y terá distribuição normal bivariada.
III. Um processo de Poisson tem incrementos independentes, mas não tem incrementos estacionários.
IV. A distribuição hipergeométrica é uma distribuição de probabilidade discreta que depende de 3 parâmetros.
Está correto o que consta APENAS em
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
Sejam Y1, Y2, Y3 as estatísticas de ordem de uma amostra aleatória de tamanho 3 de uma distribuição com função densidade dada por f(x) = e −x, para x > 0 e zero no complementar. Nessas condições, P(Y1 < 0,5) é igual a
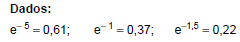
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
Para o atendimento de reclamações trabalhistas um determinado órgão público disponibilizou um único guichê de atendimento. Suponha que os requerentes cheguem ao guichê à taxa de 1/6 minutos (um a cada 6 minutos). O funcionário que atende os requerentes completa o atendimento à taxa de 1/5 minutos (um a cada 5 minutos). Considere para esse modelo de fila o M/M/1. Nessas condições, o tempo médio que cada requerente permanece na fila, em minutos, é igual a
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
Em um processo de Markov em dois estágios (zero e um) sejam:
P(Xn+1 = 0 Xn = 1) = 0,4 e P(Xn+1 = 1Xn = 0) = 0,3
Nessas condições, P(X1 = 1 X2 = 1 e X0 = 0) é igual a
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
Seja X uma variável aleatória com função densidade de probabilidade dada por: onde k é uma constate real que torna f(x) uma função densidade de probabilidade.
onde k é uma constate real que torna f(x) uma função densidade de probabilidade.
Nessas condições, a função densidade de probabilidade da variável aleatória Y = 3X + 4, no intervalo 4 < y < 10 é dada por