120 Questões de concurso encontradas
Página 10 de 24
Questões por página:
Considere que a amostra aleatória simples X1, X2, ..., Xn tenha sido retirada de uma distribuição exponencial com função de densidade na forma f(x) = λexp(–λx), em que x > 0 e λ > 0. Com relação a essa amostra e à inferência estatística, julgue o item que se segue.
De acordo com o teorema limite central, a soma 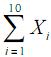 segue uma distribuição normal.
segue uma distribuição normal.
A função de distribuição acumulada da estatística de ordem X(n) = max{X1, X2, ..., Xn} é P(X(n) ≤ x) = 1 -e-λnx .
Considere que T(X1, X2, ..., Xn) seja o estimador do tipo UMVUE ( uniformly minimum-variance unbiased estimator) de λ . Nessa situação, a variância da estatística T(X1 X2, ..., Xn) corresponde ao limite inferior de Cramer-Rao.
Considere que a amostra aleatória simples X1, X2, ..., Xn tenha sido retirada de uma distribuição exponencial com função de densidade na forma f(x) = λexp(–λx), em que x > 0 e λ > 0. Com relação a essa amostra e à inferência estatística, julgue o item que se segue.
A média amostral 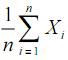 é um estimador não tendencioso do parâmetro λ.
é um estimador não tendencioso do parâmetro λ.
Considere que a amostra aleatória simples X1, X2, ..., Xn tenha sido retirada de uma distribuição exponencial com função de densidade na forma f(x) = λexp(–λx), em que x > 0 e λ > 0. Com relação a essa amostra e à inferência estatística, julgue o item que se segue.
A soma 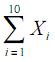 é uma estatística suficiente para a estimação do parâmetro λ
é uma estatística suficiente para a estimação do parâmetro λ