40 Questões de concurso encontradas
Página 8 de 8
Questões por página:
Dadas as matrizes A=(aij?)2×2′? sendo aij?= {2i−jj²+2?sese?i<ji≥j? e{i²−2ji²−j³?sese?i≤ji>j′? considere as afirmativas abaixo:
I. O produto da matriz M=[2 1] pela matriz A é a matriz [612?08?].
II. A soma da matriz A com a transposta de B é a matriz [22?38?].
III. A matriz M= [−3−b?−a−8?] é oposta da matriz A se a=0 e b=5.
IV. A soma dos termos da matriz A . B tais que i ≤ j é igual a 1.
V. A matriz inversa da matriz B é [0−31??31?−91??].
Estão corretas apenas as afirmativas
Seja f(x)=ax2+bx+c o polinômio de segundo grau que, dividido por x+1, x−1 e x−3, apresenta resto 8,2,52, respectivamente.
Nessas condições, qual é o valor de a+b+c ?
Analise a expressão abaixo.
(x3−x22)7
Qual é o valor do coeficiente do termo que acompanha x expandindo a expressão?
Alice parte da origem O e segue em linha reta por uma distância de a dada em quilômetros (km). Ao chegar ao final desse percurso, ela vira em um ângulo de 45º no sentido horário e anda por mais ra km. Sempre que ela chega ao final de um percurso, ela novamente vira em 45º no sentido horário, e o novo percurso terá comprimento r vezes o último percurso.
A linha poligonal simples na figura abaixo ilustra o passeio de Alice.
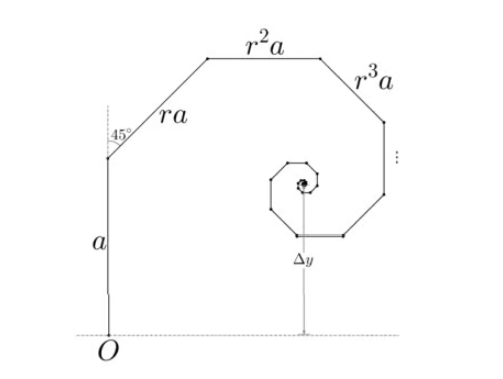
Se Alice mantiver infinitamente esse comportamento, teremos que os comprimentos dos percursos percorridos formam uma progressão geométrica infinita de razão r e termo inicial a . Considerando o problema como ilustrado na figura acima, chamaremos a medida Δy de deslocamento vertical.
Sob as condições descritas acima e considerando que a=1 km e r=21?, qual é o valor do deslocamento vertical?
A parábola determinada pela função f:R→R tal que f(x)=ax2+bx+c, com a=0, tem vértice de coordenadas V(2, −1) .
Sabendo que o ponto de coordenadas (3, 1) pertence ao gráfico dessa função, qual o valor da soma a+b+c ?