1.451 Questões de concurso encontradas
Página 177 de 291
Questões por página:
O modelo ajustado pode ser usado para calcular os valores previstos para cada indivíduo com base nas suas características x1, x2, x3 e x4. O valor esperado da variável resposta é superior a 15 e inferior a 17.
Por se tratar de uma amostra aleatória simples, espera-se que a correlação entre Xk e Yk seja nula.
Com respeito ao texto anterior, considerando uma amostragem aleatória simples (X1, Y1), (X2, Y2), ...., (Xn, Yn) para a estimação dos parâmetros da distribuição (λ > 0, φ > 0), em que cada vetor aleatório (Xk, Yk) é identicamente distribuído como (T1, T2), k = 1, 2, ..., n, julgue o item subseqüente.
Um estimador de mínimos quadrados para λ é 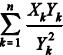
Com respeito ao texto anterior, considerando uma amostragem aleatória simples (X1, Y1), (X2, Y2), ...., (Xn, Yn) para a estimação dos parâmetros da distribuição (λ > 0, φ > 0), em que cada vetor aleatório (Xk, Yk) é identicamente distribuído como (T1, T2), k = 1, 2, ..., n, julgue o item subseqüente.
Os estimadores de máxima verossimilhança para λ e φ são, respectivamente, iguais a 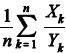 e
e 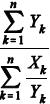 .
.
A esperança condicional pode ser escrita na forma de um modelo linear, isto é, E ( T1 T2 = t ) = αt + β , em que t > 0, ß = 0 e α = λ.

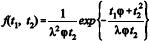 , em que t1 > 0, t2 > 0, exp( ·) representa a função exponencial, λ > 0, e φ > 0 são os parâmetros da distribuição.
, em que t1 > 0, t2 > 0, exp( ·) representa a função exponencial, λ > 0, e φ > 0 são os parâmetros da distribuição.