Uma variável aleatória Gama é definida para valores reais e positivos e sua função densidade é dada por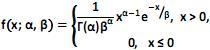

com parâmetros α > 0 e ß > 0.

Diante do exposto, analise as afirmativas.
I. Pode-se demonstrar que E(x) = αß e Var(x) = αalpha;ß².

II. A função gama é dada por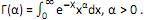

III. Pode-se mostrar que G(α) = (α – 1) G(α – 1) e para α inteiro, G(α) = (α – 1)!.

IV. Quando α = 1, a função densidade da gama e igual à distribuição exponencial com parâmetro ß.

V. Quando α = v/2 e ß = 2, com v > 0 inteiro, a função densidade da gama é igual à distribuição Qui-quadrado com v graus de liberdade.

Estão corretas apenas as afirmativas

O modelo de regressão logística é um caso particular de um modelo linear generalizado em que o componente aleatório tem distribuição Bernoulli e a função de ligação é a logito. Diante do exposto, marque V para as afirmativas verdadeiras e F para as falsas.

( ) Para uma variável explicativa numérica, o modelo logístico tem uma forma linear para o logito da probabilidade: 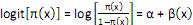, ou seja, p(x) aumenta ou diminui como uma função linear de x.
( ) A chance ou odds é a razão entre as probabilidades de sucesso e fracasso e pode ser expressa como e^α (e^ß ) ^x . Quando a variável explicativa aumenta em uma unidade, a chance é aumentada multiplicativamente por ß.
( ) Para a avaliação do modelo de regressão com variáveis explicativas numéricas pode-se utilizar a estatística X² de Pearson ou a estatística G² do teste da razão de verossimilhança dadas, respectivamente, por:



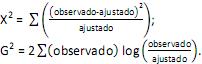
( ) Para a análise de resíduos de um modelo de regressão logística com variáveis explicativas numéricas pode-se utilizar o resíduo de Pearson ou o resíduo ajustado de Pearson, dados, respectivamente, por:



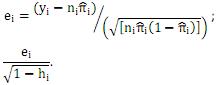
( ) O modelo de regressão logística multicategorizada é uma generalização do modelo de regressão logística, onde a variável resposta assume mais de duas categorias. Quando as categorias são nominais, escolhe-se uma como sendo a base para se construir as chances e fazer as análises necessárias. No caso de categorias ordinais, a ordenação pode ser incorporada ao modelo na forma de probabilidades acumuladas, obtendo-se, então, o modelo logito acumulativo.

A sequência está correta em

Os Modelos Lineares Generalizados (MLG) são definidos a partir de três características: o componente aleatório, que estabelece a distribuição da variável resposta; o componente sistemático, que determina as variáveis explicativas a serem utilizadas como preditoras no modelo e estabelece a equação de predição como linear; e, a função de ligação, que estabelece a relação entre o componente sistemático e a esperança matemática da variável resposta. Diante do exposto, analise.

I. O componente aleatório permite que a distribuição seja da família exponencial ou de suas generalizações, contemplando, entre outras, as distribuições: normal, Bernoulli, Poisson, Gama, Normal, Inversa, Exponencial, Binomial.
II. A função de ligação deve transformar o domínio da variável aleatória de forma a permitir que qualquer valor do componente sistemático seja admissível. As funções mais utilizadas são: identidade, inversa, inversa ao quadrado, logarítmica, logito, probito, complemento log-log, potência, Box-Cox e Aranda-Ordaz.
III. O ajuste de um MLG pode ser feito pelo método de máxima verossimilhança. As equações normais produzidas, em geral, precisam ser resolvidas por processos iterativos. Os mais utilizados são o método de Newton- Raphson e o de escore de Fisher. Eles são distintos, qualquer que seja a função de ligação.
IV. Para dados de contagem com distribuição de Poisson, o MLG corresponde ao modelo de regressão de Poisson. A função de ligação mais utilizada é a logarítmica. Quando existe superdispersão nos dados, adota-se uma generalização de MLG que admite o parâmetro de dispersão.
V. Vários tipos de resíduo podem ser utilizados para avaliar a qualidade do ajuste de um MLG, entre eles, resíduos ordinários, resíduos de Pearson, resíduos de Pearson padronizados e componente do desvio.

Estão corretas apenas as afirmativas

O modelo de análise fatorial representa a estrutura de covariância entre muitas variáveis aleatórias 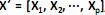, através de poucas variáveis não observáveis F´ = [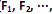 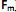] também conhecidas como fatores, construtos ou fatores comuns. Sendo E(X) = µ e V(X) = S, o modelo fatorial é expresso por X – µ = LF + e. A matriz 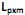é conhecida como matriz das cargas fatoriais e seus elementos, 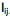, carga da variável i no fator j e as variáveis aleatórias F e em + p são não observáveis. Analise as afirmativas, marque V para as verdadeiras e F para as falsas.

( ) No modelo fatorial ortogonal, as variáveis não observáveis F e e são independentes, E(F) = 0, V(F) = E(F´F) = I, E(e) = 0, V(e) = E(e´e) = ψ. A matriz ψ é não diagonal, V(X) = S = L´L + ψ e Cov (X, F) = L.
( ) Um método de estimação para as cargas do modelo fatorial ortogonal é através de componentes principais, onde se utiliza a decomposição espectral da matriz S.
( ) Para se utilizar o método de máxima verossimilhança para estimar as cargas, é acrescida a suposição de que F e e têm distribuição normal multivariada. As comunalidades (elementos da diagonal LL´) têm como estimadores a proporção da variância total estimada pelo particular fator.
( ) Para melhorar a explicação do modelo fatorial, sem alterar a ortogonalidade dos fatores, muitas vezes, usa-se uma transformação ortogonal das cargas fatoriais, que, consequentemente, transforma os fatores. Esse procedimento é conhecido como rotação fatorial.
( ) Dependendo da natureza dos dados, os fatores não precisam ser ortogonais. Assim, para melhorar a explicação do modelo fatorial, pode-se utilizar a rotação oblíqua, onde cada variável é expressa em termos de um número máximo de fatores.
A sequência está correta em

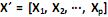O modelo de componentes principais é utilizado para representar a estrutura de variância-covariância em função de um número reduzido de combinações lineares das variáveis originais, com o objetivo de se ter uma redução de dados e uma melhor interpretação destes. Para o vetor aleatório com matriz de covariância S e autovalores iguais a 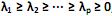, e as combinações lineares: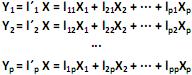



O modelo de componentes principais corresponde às combinações lineares não correlacionadas 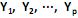com vetores de coeficientes 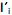de comprimento unitário, que apresentam as maiores variâncias Var 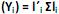. Diante do exposto, é correto afirmar que


I. o primeiro componente principal é a combinação linear 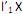que maximiza Var 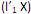sujeito a 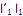= 1.

II. o i-ésimo componente principal é a combinação linear 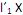que maximiza Var 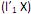= 1 e Cov (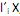, 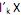) = 0, para k < i.

III. sendo 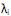os autovalores e ei os autovetores de S, o i-ésimo componente principal é dado por 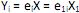+ , onde i = 1, ··· p.

IV. Var 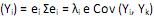= 0, para i = 1,2, ···, p e i ≠ k.

V. a proporção da variância total devido ao k-ésimo componente principal é dada por 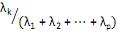para k = 1, ···, p.

Estão corretas apenas as afirmativas