60 Questões de concurso encontradas
Página 6 de 12
Questões por página:
A função de probabilidade conjunta das variáveis X e Y é dada por: f (x,y) = 1⁄32 (x2 + y2 ), x = 0,1,2,3 e y = 0,1 Nessas condições, a média de Y e P(X + Y = 3) são dados, respectivamente, por
Considere as seguintes afirmações:
I. Uma intervenção que afeta uma série temporal pode mudar o nível da série, podendo também afetar a sua variabilidade.
II. De um modo geral, a análise espectral de séries temporais estacionárias decompõe a série em componentes senoidais com coeficientes aleatórios não correlacionados.
III. Para o modelo Zt = 3 + at − 0,5at − 1, onde at é ruído branco de média zero e variância σ2, a previsão de origem t e horizonte 2 é igual a 3 − 0,5at.
IV. Se at é ruído branco de média zero e variância σ2 um modelo do tipo Zt = φZt − 12 + at, |φ| < 1, é estacionário de médias móveis sazonal.
Dentre as afirmações acima são verdadeiras APENAS
Seja 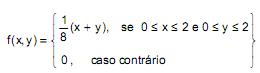 a função densidade de probabilidade da variável aleatória bidimensional contínua (X,Y). A esperança condicional de Y dado que X vale 1, denotada por E(Y | X = 1), é igual a
a função densidade de probabilidade da variável aleatória bidimensional contínua (X,Y). A esperança condicional de Y dado que X vale 1, denotada por E(Y | X = 1), é igual a
Seja X uma variável aleatória normal bivariada com vetor de médias e matriz de covariâncias dadas, respectivamente, por: 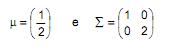
Sejam os vetores A = (2 , 0) e B = (1 , 1). Nessas condições, é verdade que a distribuição de
Uma urna contém 2 bolas verdes, 5 amarelas e 3 pretas. Selecionam-se 5 bolas aleatoriamente e sem reposição da urna. Sejam:
X = número de bolas amarelas selecionadas,
Y = número de bolas pretas selecionadas, f(x, y) a função de probabilidade da variável aleatória bidimensional (X,Y).
Nessas condições f(3,1) é igual a